[👨‍💻🇻🇳] Bubble Sort (sắp xếp nổi bọt)

Bubble Sort là một thuật toán sắp xếp kiểu so sánh rất đơn giản và dễ hiểu. Ý tưởng chính của thuật toán này là bắt cặp tất cả các phần tử trong dãy cần sắp xếp và đổi chỗ hai phần tử trong cặp nếu chúng nghịch thế (không thỏa điều kiện thứ tự).

Đối với Bubble Sort, ta chọn cặp bằng cách xét hai phần tử kế cận nhau.

Có 2 dạng sắp xếp của Bubble Sort:

Dạng 1: Sắp từ đầu đến cuối

Xuất phát từ đầu dãy, ta so sánh và đổi chỗ các cặp nghịch thế đến cuối dãy để đưa phần tử lớn nhất về cuối dãy. Khi đó chỉ việc xét các phần tử còn lại trong dãy và lặp lại các bước để sắp xếp.

Dạng 2: Sắp từ cuối lên đầu

Xuất phát từ cuối dãy, đổi chỗ các cặp phần tử nghịch thế để đưa phần tử nhỏ hơn trong cặp phần tử đó về vị trí đúng đầu dãy hiện hành, sau đó sẽ không xét đến nó ở bước tiếp theo. Lặp lại xử lý trên cho đến khi không còn cặp phần tử nào để xét.

Dạng 1: Sắp từ đầu đến cuối

int i, j;
for (i = n-1 ; i > 0; i--)
   for (j = 0; j < i; j++)
      if (a[j] > a[j+1]) //nghịch thế
         swap(a[j],a[j-1]); //đổi chổ

Dạng 2: Sắp từ cuối lên đầu

int i, j;
for (i = 0; i < n-1; i++)
   for (j = n-1; j > i; j--)
      if (a[j-1] > a[j]) //nghịch thế
         swap(a[j],a[j-1]); //đổi chỗ

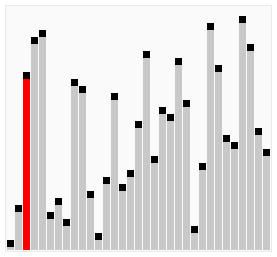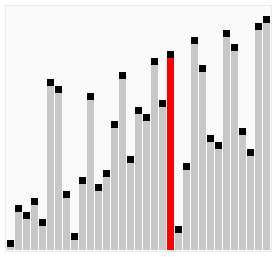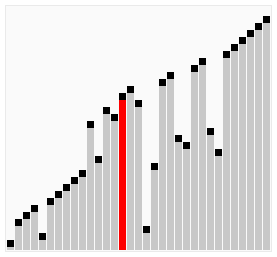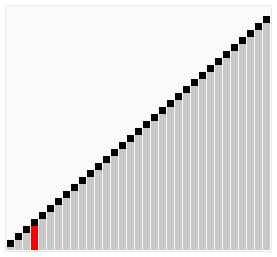
Dưới đây là minh hoạ cho thuật toán Bubble Sort theo dạng 1 (nguồn: Wikipedia).

Số phép so sánh không phụ thuộc vào tình trạng ban đầu của dãy. Có thể ước lượng số phép so sánh bằng: $(n-1) + (n-2) + … + 1 = n(n – 1)/2$.

Số phép hoán vị (3 phép gán) phụ thuộc tình trạng ban đầu. Trong trường hợp tốt nhất, tức dãy đã được sắp xếp hoàn toàn thì không cần phải hoán vị, nên số phép hoán vị là: 0.

Trường hợp xấu nhất, tức dãy có thứ tự ngược với yêu cầu. Mỗi lần so sánh ta lại phải hoán vị nên số phép hoán vị là: $n(n – 1)/2$.

Độ phức tạp của thuật toán này là: $O(n^2)$.