Danh sách liên kết là một cấu trúc dữ liệu mà mỗi phần tử cần phải lưu thông tin của nó và địa chỉ của phần tử kế tiếp hoặc trước nó. Danh sách liên kết linh động hơn mảng rất nhiều do có thể thêm, xóa phần tử. Có nhiều dạng danh sách liên kết khác nhau và ở phần này mình sẽ nói về danh sách liên kết đơn cùng các thao tác với nó (minh họa bằng C++).
Mỗi phần tử trong DSLK đơn (gọi là node hay nút) sẽ gồm một biến lưu dữ liệu của bạn và một biến con trỏ lưu địa chỉ của phần tử kế tiếp. Các phần tử được liên kết với nhau dựa vào con trỏ này.
struct Node
{
<kiểu dữ liệu> info;
Node *next;
};
Như vậy, khi biết được phần tử đầu danh sách thì dựa vào con trỏ next, ta có thể truy cập được tất cả các phần tử trong danh sách. Vậy một danh sách chỉ gồm 1 con trỏ trỏ đến phần tử đầu danh sách. Tuy nhiên, để một vài thao tác trở nên dễ dàng, ta có thể thêm một con trỏ đến cuối danh sách.
struct List
{
Node *head, *tail;
};
Nếu chưa hiểu cấu trúc của nó, bạn có thể xem hình minh họa sau.
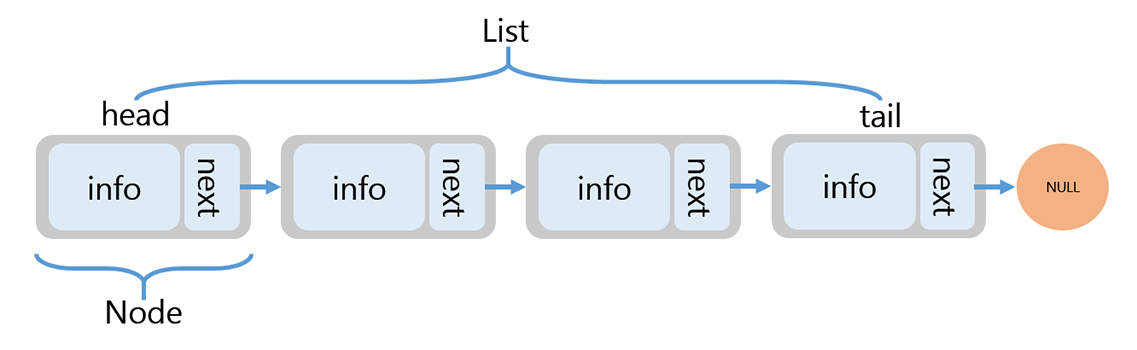
Contents
Tạo danh sách rỗng
Tại sao đây lại là một thao tác quan trọng. Một danh sách được tạo ra chứa 2 con trỏ rỗng chưa trỏ đến đâu cả. Vì vậy sẽ rất nguy hiểm nếu thao tác với 2 con trỏ này. Cần thiết phải gán cho nó giá trị NULL trước khi thao tác trên nó. Nếu bạn cài đặt danh sách theo phương pháp hướng đối tượng thì có thể khai báo phần này trong constructor nên không cần gọi hàm này bên ngoài.
void CreateList(List &list)
{
list.head = list.tail = NULL;
}
Tạo nút với dữ liệu của bạn
Công việc này giống như biến dữ liệu của bạn thành một phần tử để đưa vào danh sách.
Node* CreateNode(<kiểu dữ liệu> data)
{
Node* node = new Node;
if (node)
{
node->info = data;
node->next = NULL;
}
return node;
}
Có thể vì một số nguyên nhân khách quan (tình trạng hệ thống, bộ nhớ,…) mà biến node không cấp phát động được, vì vậy cần thiết kiểm tra xem node được cấp phát có khác NULL hay không.
Thêm nút vào danh sách
Có 3 cách thêm vào: đầu danh sách, cuối danh sách và sau một phần tử trong danh sách. Với mỗi trường hợp ta xét trường hợp danh sách rỗng và danh sách có phần tử.
Nguyên tắc chung để thêm vào: điều chỉnh liên kết của node mới -> điều chỉnh liên kết của node có sẵn tại vị trí thêm vào -> sửa lại con trỏ của danh sách (nếu cần).
void AddHead(List &list, Node* node)
{
if (!list.head) //xét danh sách rỗng
list.head = list.tail = node;
else
{
node->next = list.head; //sửa lk node cần thêm
list.head = node; //chỉnh lại con trỏ của danh sách
}
}
void AddTail(List &list, Node* node)
{
if (!list.head)
list.head = list.tail = node;
else
{
list.tail->next = node;
list.tail = node;
}
}
void AddAfter(List &list, Node *node, Node *before)
{
if (!before)
{
node->next = before->next; //sửa liên kết của node mới
before->next = node; //sửa lại lk của node có sẵn
if (list.tail == before)
list.tail = node; //sửa lại con trỏ chỉ danh sách
}
else
AddHead(list, node);
}
Duyệt danh sách
Thao tác này rất thường gặp trong việc đếm hay in ra màn hình, v.v… Danh sách liên kết được duyệt bằng cách ghé thăm tuần tự từng node trong danh sách. Bạn có thể dùng vòng while hay for đều được.
Node *i = list.head;
while (i)
{
//thao tác
i = i->next;
}
for(Node *i = list.head; i ; i = i->next)
{
//thao tác
}
Tìm phần tử
Để tìm một phần tử nào đó ta cũng dùng phương pháp duyệt. Ví dụ dưới đây là tìm một phần tử có khóa key theo phương pháp tìm kiếm tuần tự.
Node* Search(List list, int key)
{
Node *i = list.head;
while (i && i->info != key)
i = i->next;
return i;
}
Hủy phần tử và hủy cả danh sách
Ở đây ta xét hủy phần tử đầu, hủy phần tử cuối, hủy phần tử sau một node, hủy phần tử có theo khóa và hủy cả danh sách. Khi hủy phần tử ta phải xét theo 3 trường hợp: danh sách rỗng, danh sách có 1 phần tử, danh sách nhiều phần tử.
Nguyên tắc hủy cơ bản là: cô lập phần tử cần hủy, sau đó chỉnh sửa lại liên kết cho đúng và cuối cùng là xóa phần tử khỏi bộ nhớ.
void RemoveHead(List &list)
{
if (!list.head)
cout << "Empty list!" << endl;
else if (list.head == list.tail)
{
delete list.head;
list.head = list.tail = NULL;
}
else
{
Node *temp = list.head;
list.head = list.head->pNext;
delete temp;
}
}
Khi xóa 1 phần tử ta cần phải biết phần tử trước nó để có thể điều chỉnh lại liên kết cho phù hợp. Mà mỗi phần tử lại chỉ biết phần tử đứng sau mà không biết được phần tử đứng trước vì vậy cần phải duyệt tìm phần tử đứng trước tail mới có thể hủy phần tử cuối được.
void RemoveTail(List &list)
{
if (!list.head)
cout << "Empty list!" << endl;
else if (list.head == list.tail)
{
delete list.head;
list.head = list.tail = NULL;
}
else
{
Node *temp = list.head;
while (temp->next != list.tail)
temp = temp->next;
delete list.tail;
list.tail = temp;
}
}
Tương tự với hủy phần tử sau 1 node, hủy phần tử theo dữ liệu và hủy cả danh sách.
void RemoveAfter(List &list, Node *node)
{
if (!list.head)
cout << "Empty list!" << endl;
else
{
Node *temp = node->next;
if (temp)
{
node->next = temp->next;
delete temp;
}
}
}
void RemoveKey(List &list, int key)
{
if (!list.head)
cout << "Empty list!" << endl;
else
{
Node *result = list.head, *before = NULL;
while (result && result->info != key)
{
before = result;
result = result->next;
}
if (result)
{
if (result == list.head)
RemoveHead(list);
else
RemoveAfter(list, before);
}
}
}
void RemoveList(List &list)
{
Node *i = list.head;
while (list.head)
{
i = i->next;
delete list.head;
list.head = i;
}
list.head = list.tail = NULL;
}
Sắp xếp danh sách
Có 2 kiểu sắp xếp:
- Đổi dữ liệu các node: Kiểu sắp xếp này tương tự như sắp xếp mảng. Ưu điểm là cài đặt đơn giản nhưng hiệu quả không hơn gì sắp xếp trên mảng. Các thuật toán phù hợp là: Interchange Sort, Bubble Sort, Selection Sort và Insertion Sort.
- Đổi các liên kết giữa các node: Kiểu sắp xếp này cài đặt rất phức tạp nhưng lại tận dụng được ưu điểm của DSLK, vì vậy nó hiệu quả hơn kiểu sắp xếp trên. Các thuật toán phù hợp: Quick Sort, Merge Sort, Radix Sort, …
#Danh #sách #liên #kết #đơn #và #các #thao #tác #cơ #bản




![[👨💻🇻🇳] Danh sách liên kết đơn và các thao tác cơ bản](https://i0.wp.com/2023-data-image.dreamhosters.com/wp-content/uploads/sites/3/2024/03/11705365_588694987938979_4818411244690248758_n.jpg?w=960&resize=960,539)
![[👨💻🇻🇳] Danh sách liên kết đơn và các thao tác cơ bản](https://i0.wp.com/2023-data-image.dreamhosters.com/wp-content/uploads/sites/3/2024/03/11659520_589271447881333_4147216583258866097_n.jpg?w=960&resize=960,539)
![[👗🇻🇳] IVY moda – Chuỗi thương hiệu thời trang công sở 👕 Top1Fashion 👗 – New Arrival: Sơ mi Grace x Chân váy tweed
Sự kết hợp hoàn hảo giữa áo sơ mi các …](https://i0.wp.com/2023-data-image.dreamhosters.com/wp-content/uploads/sites/3/2024/09/460044434_927493252745997_3467836758117151314_n.jpg?w=336&resize=336,220)
![Hạt é kỵ với gì? Lợi ích của loại hạt nhỏ mà “có võ” [🆕🇻🇳] bazaarvietnam.vn](https://i0.wp.com/2023-data-image.dreamhosters.com/wp-content/uploads/sites/3/2024/09/2024_shop1_top1vietnam_top1list_top1index_harper-bazaar-hat-e-ky-voi-gi-4.jpg?w=336&resize=336,220)
![[🆕🇻🇳] [HOT] Cập nhật “diện mạo” của iPhone 16 mới ra mắt của Apple](https://i2.wp.com/2023-data-image.dreamhosters.com/wp-content/uploads/sites/3/2024/09/2024_shop1_top1vietnam_top1list_top1index_Dien-mao-iphone-16.jpg?w=336&resize=336,220)
![[🆕🇻🇳] Có nên nâng cấp iPhone 15 Pro lên iPhone 16 Pro?](https://i0.wp.com/2023-data-image.dreamhosters.com/wp-content/uploads/sites/3/2024/09/2024_shop1_top1vietnam_top1list_top1index_Iphone_16_gia_bao_nhieu.jpg?w=336&resize=336,220)
